电磁流体力学

针对微流控芯片、新型电池技术、电磁信号探测、高超声速流动等不同应用场景，提炼其中的关键科学问题，发展电磁场-流场耦合的数学理论和数值计算方法。

G Li et al., Phys. Rev. Lett. 2019 

G Li & D Koch, J. Fluid Mech. 2020 

G Li et al. Phys. Rev. Fluids 2021 

G Li et al. J. Fluid Mech. 2022

微尺度流动

微尺度流动广泛存在于微生物运动、微加工技术、生物制药技术、化学工业等问题中。受界面效应、布朗运动、复杂流体效应等作用，微尺度流动常表现出不同于宏观流动的特征。深入研究这些独特的流体现象，将进一步推动微操作和微加工技术的发展，实现常规方法所难以完成的功能。

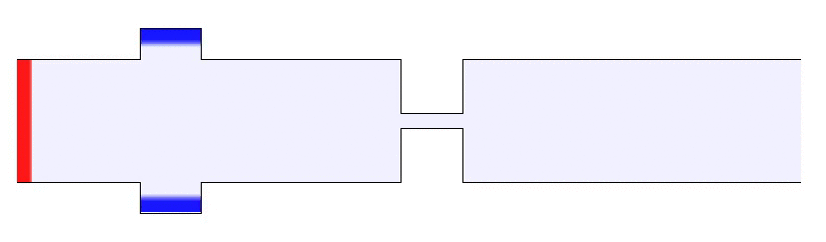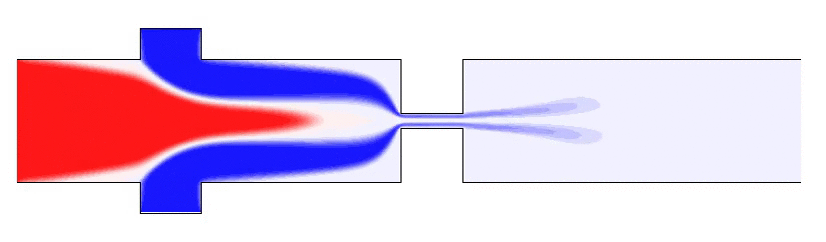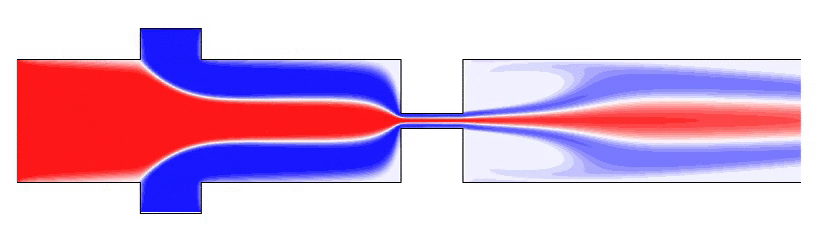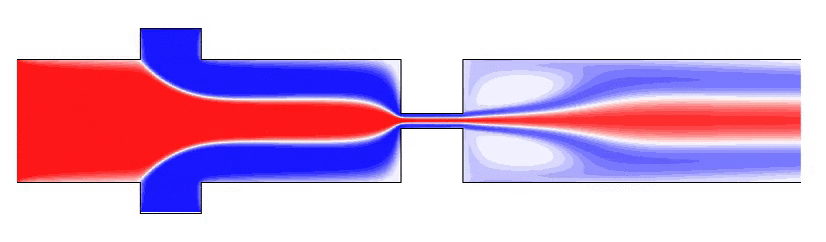
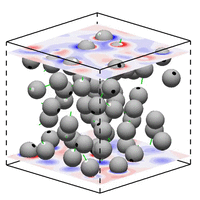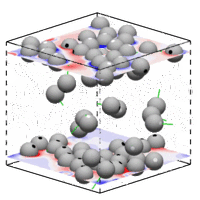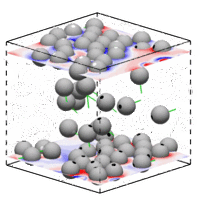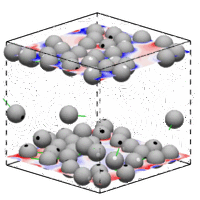
G Li & A Ardekani, Phys. Rev. E 2014

G Li et al., Rheol. Acta 2014

G Li et al., J. Fluid Mech. 2015

G Li & A Ardekani, J. Fluid Mech. 2015

G Li et al., Phys. Rev. E 2016

G Li & A Ardekani, Phys. Rev. Lett. 2016

G Li et al. J. Nonnewton. Fluid Mech. 2021

G Li, J. Fluid Mech. 2022

仿生流体力学

与自然界中生物的飞行、游动方式相比，人类现有的技术方式在高速、高载荷等方面具有显著优势。但在一些非传统应用场景中，生物的运动方式具有低能耗、低可探测性、高机动性方面的优势，因而愈发受到人们的重视。如何利用力学分析和机械加工手段，实现新型仿生设计与现有电子、机械技术的有机结合，是本研究的核心。

G Li & X Lu, J. Fluid Mech. 2012

G Li et al., J. Hydrodynam. 2012

G Li et al., Acta Mech. Sin. 2014

多相流和高分子流动

多相流和高分子流动广泛存在于人们的日常生活和工业应用中。其中涉及界面演化、多体相互作用、传热传质过程、多尺度流场结构演化等复杂问题，本研究主要通过数值模拟分析解释复杂现象背后的关键物理规律。

数值方法研究

基于有限体积、有限元、边界元、谱方法等数值模拟方法，发展高效、高精度的数值程序，解决不同的科学问题。