CPU / GPU software for fast simulation of Scanning Transmission Electron Microscopy (STEM) experiments

Prismatic is the name of our simulation code which performs quantum-mechanical simulation of images and diffraction patterns for scanning transmission electron microscopy (STEM). STEM experiments are routinely used for atomic-resolution imaging of samples in materials science and other fields. STEM simulations are difficult primarily because of the "scanning" aspect, where the electron probe is moved over the sample surface - each new probe location requires a full multiple-scattering simulation, and STEM images often contain millions of pixels.

Prismatic is a CUDA/C++/Python software package for fast image simulation in scanning transmission electron microscopy (STEM) and high-resolution transmission electron microscopy (HRTEM). It includes parallel, data-streaming implementations of both the plane-wave reciprocal-space interpolated scattering matrix (PRISM) and multislice algorithms using multicore CPUs and CUDA-enabled GPU(s), in some cases achieving accelerations as high as 1000x or more relative to traditional methods. Prismatic is fast, free, open-sourced, and contains a graphical user interface.

Prismatic is an implementation of two related algorithms for STEM and HRTEM simulation:

• Multislice

  In this method, we use first compute the projected potentials from a set of atomic coordinates. Next, for all STEM probes, we solve the Schrodinger equation for fast electrons using a split-step method, where we alternate between the transmission operator (which gives the phase shift atoms impart onto the electron wave) and the propagation operator (describing free-space propagation of the electron wave).

• PRISM

  Multslice STEM simulations can be quite slow, because the scattering of each new STEM probe is recomputed from scratch. An alternative is to use the multislice method to compute a scattering matrix, which is then used to construct each STEM probe. This algorithm often requires roughly the same computational time as the mutlislice method, but also allows for huge speed-ups by using Fourier interpolation of the scattering matrix. Thus we call this approach the plane-wave recriprocal-space interpolated scattering matrix (PRISM) algorithm.

Website: Prismatic Software For STEM Simulation(prism-em.com)

REal Space Iterative Reconstruction (RESIRE)

Tomography has made a revolutionary impact on the physical, biological and medical sciences. The mathematical foundation of tomography is to reconstruct a three-dimensional (3D) object from a set of two-dimensional (2D) projections. As the number of projections that can be measured from a sample is usually limited by the tolerable radiation dose and/or the geometric constraint on the tilt range, a main challenge in tomography is to achieve the best possible 3D reconstruction from a limited number of projections with noise. Over the years, a number of tomographic reconstruction methods have been developed including direct inversion, real-space, and Fourier-based iterative algorithms. Here, we report the development of a real-space iterative reconstruction (RESIRE) algorithm for accurate tomographic reconstruction. RESIRE iterates between the update of a reconstructed 3D object and the measured projections using a forward and back projection step. The forward projection step is implemented by the Fourier slice theorem or the Radon transform, and the back projection step by a linear transformation. Our numerical and experimental results demonstrate that RESIRE performs more accurate 3D reconstructions than other existing tomographic algorithms, when there are a limited number of projections with noise. Furthermore, RESIRE can be used to reconstruct the 3D structure of extended objects as demonstrated by the determination of the 3D atomic structure of an amorphous Ta thin film. We expect that RESIRE can be widely employed in the tomography applications in different fields. Finally, to make the method accessible to the general user community, the MATLAB source code of RESIRE and all the simulated and experimental data are available at https://zenodo.org/record/7273314.

GENFIRE: A generalized Fourier iterative reconstruction algorithm for high-resolution 3D imaging

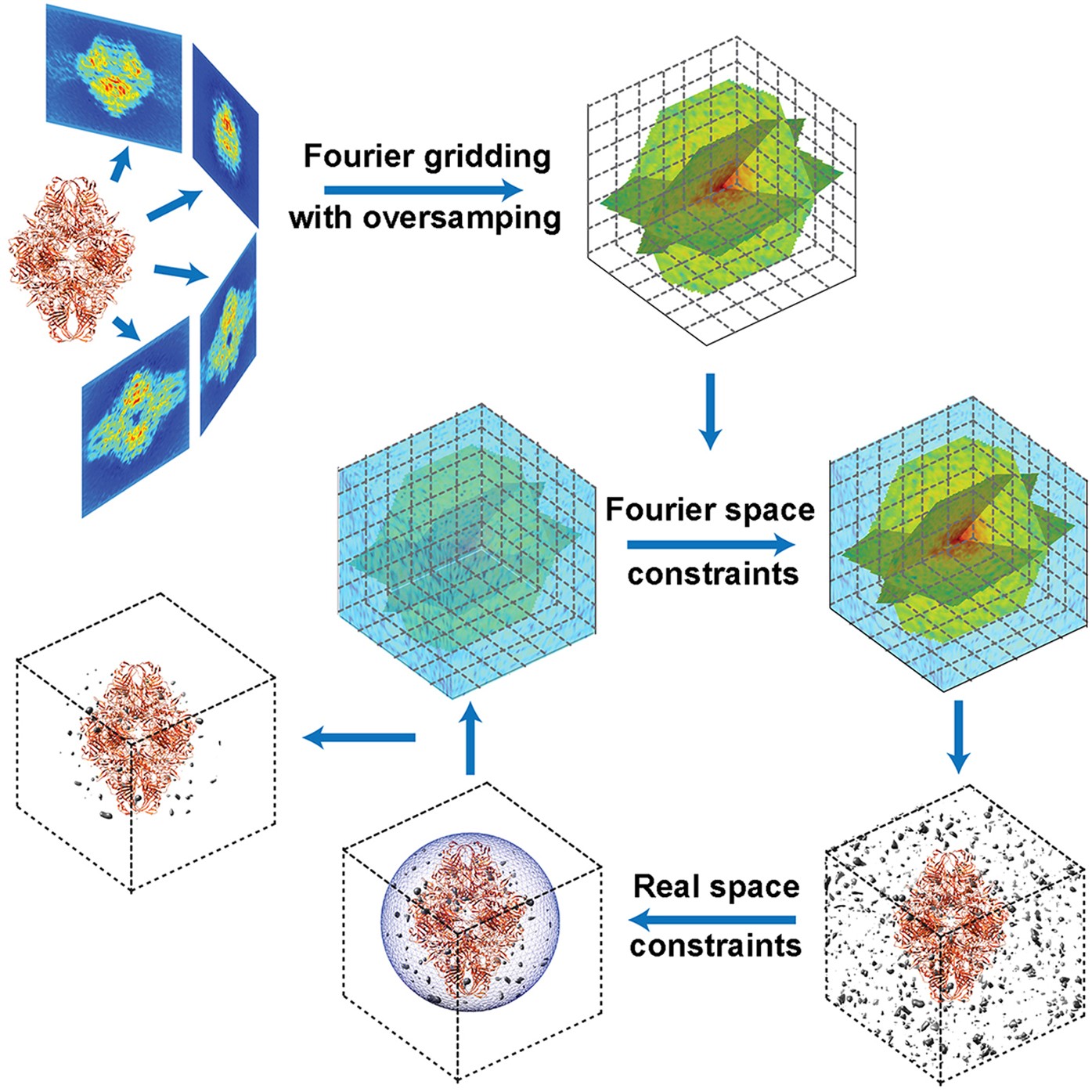
Tomography has made a radical impact on diverse fields ranging from the study of 3D atomic arrangements in matter to the study of human health in medicine. Despite its very diverse applications, the core of tomography remains the same, that is, a mathematical method must be implemented to reconstruct the 3D structure of an object from a number of 2D projections. Here, we present the mathematical implementation of a tomographic algorithm, termed GENeralized Fourier Iterative REconstruction (GENFIRE), for high-resolution 3D reconstruction from a limited number of 2D projections. GENFIRE first assembles a 3D Fourier grid with oversampling and then iterates between real and reciprocal space to search for a global solution that is concurrently consistent with the measured data and general physical constraints. The algorithm requires minimal human intervention and also incorporates angular refinement to reduce the tilt angle error. We demonstrate that GENFIRE can produce superior results relative to several other popular tomographic reconstruction techniques through numerical simulations and by experimentally reconstructing the 3D structure of a porous material and a frozen-hydrated marine cyanobacterium. Equipped with a graphical user interface, GENFIRE is freely available from our website and is expected to find broad applications across different disciplines.

Website: GENeralized Fourier Iterative REconstruction